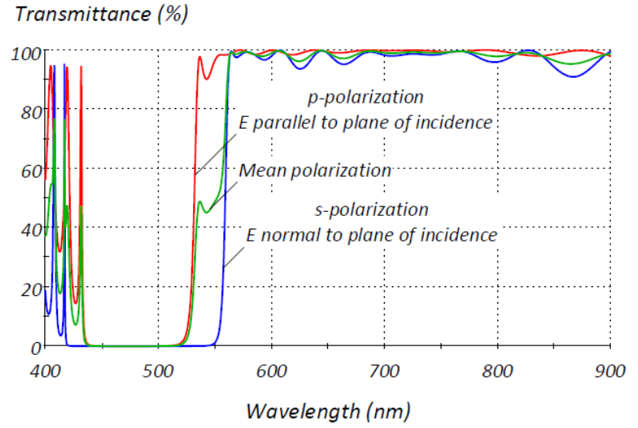
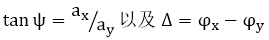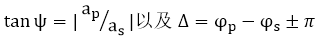我們用偏振來(lái)描述光波電(diàn)場(chǎng)的方向。雖然是很(hěn)複雜,但(dàn)它的影(yǐng)響是完全明(míng)确和(hé)可(kě)計(jì)算(suàn)的。圖1顯示了一個(gè)簡單的長波通(tōng)濾波器(qì)在斜入射時(shí)的計(jì)算(suàn)性能,其曲線标記為(wèi)p-偏振、s-偏振和(hé)平均極化。這些(xiē)名稱是什麽意思?
圖1. 在45°條件下計(jì)算(suàn)的600nm長波通(tōng)濾光片,顯示了P偏振、S偏振和(hé)平均偏振的透射率。
讓我們将討(tǎo)論局限于完全各向同性的材料。所涉及的過程是線性的,允許我們将任何問題分解為(wèi)一系列可(kě)以單獨遵循的簡單分量。對于Essential Macleod中的所有(yǒu)計(jì)算(suàn),基本分量是線偏振平面波(或單色光)。
當我們討(tǎo)論偏振時(shí),我們經常提到線偏振或平面偏振、圓偏振和(hé)橢圓偏振。在計(jì)算(suàn)中,所有(yǒu)這些(xiē)偏振被表示為(wèi)兩個(gè)正交線偏振的組合,其可(kě)以單獨計(jì)算(suàn)并且在透射或反射中的取向不變。它們有(yǒu)時(shí)被稱為(wèi)偏振的本征模式,這在斜入射時(shí)尤為(wèi)重要。光學薄膜的作(zuò)用是改變每種組分的振幅和(hé)相位。膜層的性能量化了這些(xiē)變化。
如果沒有(yǒu)參考系,那(nà)麽這些(xiē)性能參數(shù)是沒有(yǒu)意義的,我們需要定義基準軸,電(diàn)場(chǎng)的正方向,以及我們比較相位的點。Z軸垂直于膜層表面,其正方向與入射方向一緻。X軸沿着膜層表面,與Z軸一起定義入射面。原點是Z軸與前表面面或入射面的交點。我們通(tōng)常将入射面可(kě)視(shì)化為(wèi)顯示系統的平面,Y軸垂直于顯示器(qì),并向外指向觀察者。
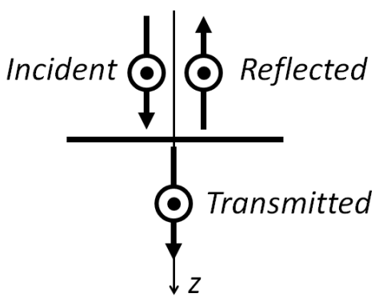
在垂直入射時(shí),對線性偏振方向影(yǐng)響,因此我們将入射波中的電(diàn)場(chǎng)的正方向設置為(wèi)沿着正y軸。相同的慣例适用于反射波和(hé)透射波。對于相位參考點,我們選擇入射波和(hé)反射波的坐(zuò)标原點,但(dàn)是z軸從發射波的後表面或出射表面出現的點,我們選擇時(shí)間(jiān)變量,使入射波的相位在參考點處為(wèi)零。然後,反射和(hé)透射波的相位也就是反射和(hé)透射的相位變化。圖2顯示了這種約定。
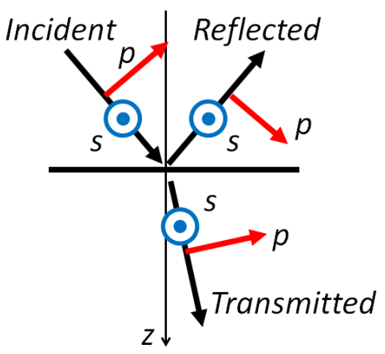
我們約定中的不連續性會(huì)造成很(hěn)大(dà)的困難,因此我們确保斜入射約定與正常入射約定兼容。我們需要一個(gè)s和(hé)p偏振的約定,因此選擇電(diàn)場(chǎng)的正方向,如圖3所示。很(hěn)明(míng)顯,這一慣例在正常情況下崩潰,如圖2所示。
圖2. 電(diàn)矢量正方向的垂直入射慣例。這适用于所有(yǒu)可(kě)能的線偏振方向。
圖3. p和(hé)s偏振的電(diàn)矢量正方向的慣例。
反射率R和(hé)透射率T是計(jì)算(suàn)的重要參數(shù),我們必須小(xiǎo)心它們在斜入射時(shí)的定義。所涉及的光是無限大(dà)的平面波,它們超出了我們的接收器(qì)。在沒有(yǒu)吸收的情況下,我們希望R和(hé)T相加等于一個(gè)單位(或100%),但(dàn)是由于折射以及接收器(qì)位置的原因,這将無法實現。因此,我們在計(jì)算(suàn)中使用輻照度的垂直分量。當光束直徑小(xiǎo)于接收器(qì)的光束直徑時(shí),該定義與使用受限光束(例如來(lái)自激光器(qì)的光束)的測量完全一緻。
除了反射率和(hé)透射率外,其他基本參數(shù)是參考點處反射波和(hé)透射波相對于入射波相位的變化。
Paul Drude在19世紀末發明(míng)了橢圓偏振光譜法,作(zuò)為(wèi)測量金屬光學常數(shù)的技(jì)術(shù)。測量橢圓偏振的形狀僅涉及相對測量,避免了絕對測量的巨大(dà)困難。定義橢圓需要兩個(gè)量,它們可(kě)以采用不同的形式。 橢圓度和(hé)方向角是兩個(gè)這樣的量,但(dàn)最常見的是沿兩個(gè)定義的參考軸測量的振幅的比率及其相對相位。 不幸的是,振幅比可(kě)以從零到無窮大(dà)變化,這是一個(gè)困難的範圍,更合适的數(shù)量是它的反正切。 如果參考方向是x,y和(hé)z,則z是沿着傳播方向,當我們定義兩個(gè)角度量時(shí),ψ(psi)和(hé)Δ(delta)為(wèi)
a和(hé)φ分别代表幅度和(hé)相位。光學膜層的反射和(hé)透射會(huì)影(yǐng)響ψ和(hé)Δ的值,如果選擇p和(hé)s方向作(zuò)為(wèi)參考方向,則可(kě)以簡化計(jì)算(suàn)。那(nà)麽與表面相關的tanψ值是p和(hé)s偏振的幅度變化的比率的絕對值,Δ值是相位變化的差值。如果參考方向在入射波中的方向相似,則将舊(jiù)的tanψ乘以膜層的tanψ,并将舊(jiù)的Δ加到膜層的Δ上(shàng),得(de)到新的參數(shù)。然而,存在一個(gè)小(xiǎo)問題,稱為(wèi)奇偶校(xiào)驗偏移。
當我們觀察鏡子中物體(tǐ)的反射時(shí),我們看到的圖像與物體(tǐ)不完全相同,通(tōng)常我們将其視(shì)為(wèi)左右交換。無論我們解釋它的哪種方式,右手系統的軸都變為(wèi)左手,這也适用于我們的橢圓偏振參數(shù)突然的左手反射。通(tōng)常采用的一種解決方案是反轉反射中p偏振的正方向,但(dàn)不是薄膜計(jì)算(suàn)的良好解決方案。 為(wèi)了保持一緻性,我們應該在垂直入射時(shí)反轉反射的p方向,但(dàn)是如果沒有(yǒu)入射平面我們怎麽能這樣做(zuò)呢? 我們選擇更簡單的解決方案。 保留我們對p和(hé)s方向的定義,我們在反射中定義橢圓參數(shù),但(dàn)不在透射中定義
這是Essential Macleod中使用的定義。 注意,Δ也稱為(wèi)相對延遲,或者有(yǒu)時(shí)簡稱為(wèi)延遲。在垂直入射時(shí),tanψ是1,因此ψ是45°,并且由于奇偶校(xiào)驗位移,Δ是180°。這些(xiē)橢圓量也可(kě)以作(zuò)為(wèi)優化目标輸入。
對于非偏振光,在p方向和(hé)s方向之間(jiān)沒有(yǒu)相位關系,但(dàn)是在傾斜入射時(shí)将存在偏振效應。如果接收器(qì)對偏振不敏感,那(nà)麽該測量将對應于p和(hé)s偏振的平均值。由于兩種模式的性能通(tōng)常不同,因此将存在有(yǒu)效的ψ,并且也可(kě)以計(jì)算(suàn)。
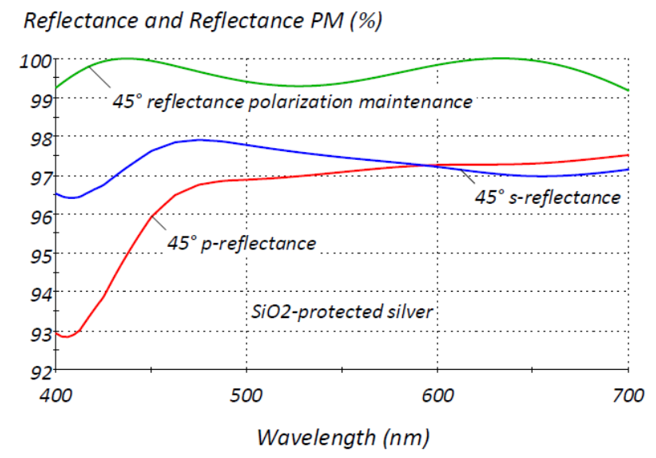
斜入射對偏振的敏感度在光學系統中可(kě)能會(huì)出現一些(xiē)困難的問題。Polarization Maintenance(PM)是我們用來(lái)量化分量或系統保持偏振功能的術(shù)語,如圖4所示。與入射面成45°角的線偏振光,由一個(gè)完善的系統反射或透射,輸出時(shí)将保持不變。ψ将保持在45°和(hé)Δ在0°或180°之間(jiān),取決于奇偶校(xiào)驗。我們通(tōng)過測量所需方向的輸出輻照度和(hé)任何正交偏振光的輸出輻照度來(lái)檢查這一點,并将PM定義為(wèi)所需偏振模式的輻照度與總輻照度之比,其比例為(wèi)0至100.0%。PM是一個(gè)可(kě)優化的量。
圖4. 115nm SiO2保護膜銀反射鏡在45°入射時(shí)的反射和(hé)反射PM。
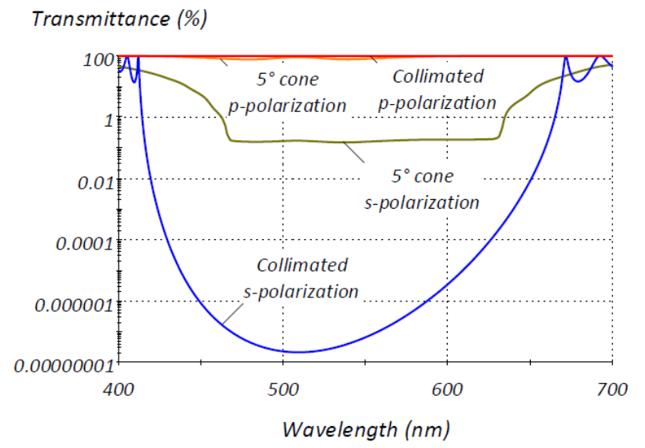
可(kě)以在堆棧文檔或包含介質的設計(jì)中進行(xíng)錐角光源入射計(jì)算(suàn)。在這裏,我們相對于入射光的軸向光線及其入射平面定義p和(hé)s偏振。無論偏振是什麽,接收器(qì)都測量總輻照度。錐角光線中的偏斜光線具有(yǒu)局部入射平面,并且它們的p和(hé)s方向可(kě)以與軸向光線不同,從而導緻錐體(tǐ)的偏振模式之間(jiān)的洩漏。如圖5
圖5. 由準直光和(hé)5°錐角照射的31層立方體(tǐ)偏振器(qì)。
Essential Macleod中有(yǒu)一些(xiē)規定包括雙折射層材料。它們的主方向的取向必須與參考軸一緻。
|