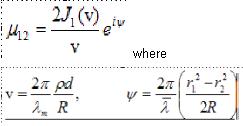FRED将高(gāo)斯光分束運算(suàn)法則運用于傳播相幹光場(chǎng)通(tōng)過系統幾何模型。這裏我們來(lái)看一下這項性能的示範。

高(gāo)斯光分束（GBD）的綜合形式使得(de)FRED可(kě)以對廣泛的物理(lǐ)光學現象進行(xíng)解釋。在過去的1/4世紀裏，GBD運算(suàn)法則已被證明(míng)在模拟衍射和(hé)幹涉效應上(shàng)具有(yǒu)顯著的精确性。這裏我們演示FRED的GBD性能用于說明(míng)部分相幹，我們來(lái)觀察一個(gè)衍射計(jì)的例子。

衍射計(jì)[1],[2]是演示部分相幹性很(hěn)有(yǒu)用的一個(gè)儀器(qì)。實驗結構裝置可(kě)以用下圖表示。擴展非相幹光源S0通(tōng)過透鏡L0成像于S1。由S1出來(lái)的光線通(tōng)過L1準直并通(tōng)過透鏡L2聚焦于平面F上(shàng)。包含兩孔徑P1和(hé)P2的非透明(míng)屏A置于透鏡L1和(hé)L2中間(jiān)。孔徑P1和(hé)P2可(kě)以為(wèi)任何形狀、尺寸和(hé)位置。

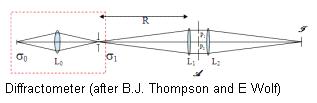
在FRED模型中，如上(shàng)圖中紅色虛線所圈出部分用于收集點光源随機發出的不同波長的光線，它的作(zuò)用類似于小(xiǎo)孔區(qū)域的S1。這種收集而來(lái)的光線類似于Born & Wolf提出的準單色光源。在平面F上(shàng)，光源中的不同波長形成了幹涉圖。通(tōng)過設計(jì)，FRED演示了相同波長的相幹性和(hé)不同波長之間(jiān)的非相幹。因此，在F面上(shàng)的總照度圖形成了不同相幹成分下的非相幹的總和(hé)。

根據由P.H. van Cittert在 1934 和(hé) F. Zernike 在 1938提出重要的部分相幹理(lǐ)論的獨立發展，在S1 處的光源收集引起了在A處屏上(shàng)兩點P1和(hé)P2之間(jiān)的場(chǎng)産生(shēng)了相關性。先驅的Cittert-Zernike法則确定了以下部分相幹的關系式：

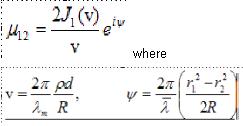
這裏r是小(xiǎo)孔S1的半徑，d是兩孔P1和(hé)P2的中心距離。R是透鏡L1的焦距，r1和(hé)r2是孔P1和(hé)P2離開(kāi)光軸的距離，而Im是平均波長。

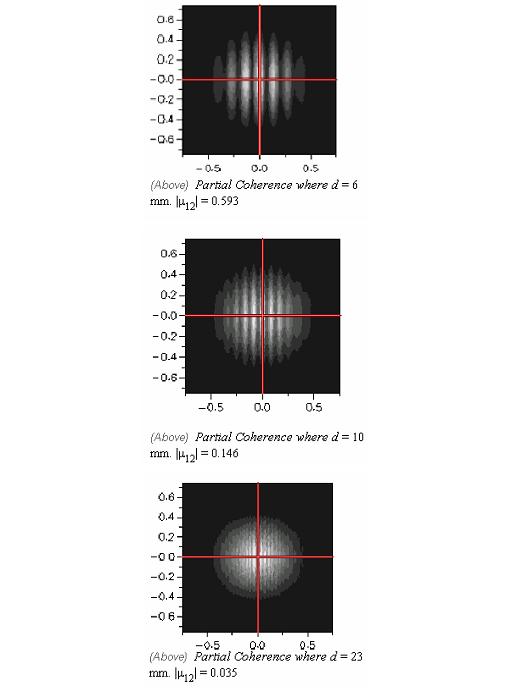
作(zuò)為(wèi)測試FRED的性能，我們已經得(de)出了和(hé)Thompson and Wolf通(tōng)過計(jì)算(suàn)在分開(kāi)距離為(wèi)d的小(xiǎo)孔P1和(hé)P2，在平面F上(shàng)的照度計(jì)算(suàn)吻合的結果。相關的參數(shù)為(wèi)f1=f2=1520mm;透鏡L1和(hé)L2分開(kāi)14mm，小(xiǎo)孔S1的直徑為(wèi)90mm，孔徑P1,P2的直徑為(wèi)1.4mm;平均波長為(wèi)Im=0.579mm。以下圖中顯示了d=6,10和(hé)23mm時(shí)的照度圖和(hé)|u12|=0.593，.146和(hé)0.035.

[1] Born & Wolfe, Principle of Optics (6th Ed), Pergamon Press, Ch. 10, Sec. 4.3, p. 513

[2] B.J. Thompson & E. Wolf, J. Opt. Soc. Amer., 47 (1957), p.895.