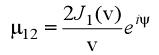RED在高(gāo)斯光線分解理(lǐ)論(GBD)的一個(gè)普遍形式下可(kě)以對形形色色物理(lǐ)光學現象做(zuò)出合理(lǐ)的解釋。在過去的25年間(jiān),經過改進的GBD算(suàn)法,已經可(kě)以精确的模拟衍射和(hé)幹涉現象,并且與事實忠實的吻合。這種完美的藝術(shù)是它在模拟用衍射儀觀察泰伯效應和(hé)局部相幹性上(shàng)的應用的一個(gè)很(hěn)好的例子。
GBD背後的基礎是1969年被Arnaud首先提出的,他提出:一個(gè)任意波可(kě)以由一組高(gāo)斯光線的基礎組合而合成,而那(nà)些(xiē)高(gāo)斯光線可(kě)以用射線來(lái)追蹤。普通(tōng)的GBD方法在兩種極端條件下限制(zhì)了這種合成。當光線被放置在平行(xíng)隙縫的光栅上(shàng),它會(huì)發生(shēng)一種特殊的分解,或者在一種空(kōng)間(jiān)頻譜含量的條件下發生(shēng)傅裏葉分解。後來(lái)Gabor延伸拓展了Arnaud的方法,FRED應用這種拓展使這兩種方法結合成一種,以便更靈活的适應更寬範圍的的條件。
泰伯效應
泰伯效應是由近場(chǎng)衍射産生(shēng)的,在光線接近光栅或者其它周期性結構時(shí)可(kě)以觀察到。在變化的衍射極之間(jiān)産生(shēng)的幹涉使周期性結構沿着傳播方向上(shàng)在他們各自的泰伯距離處自成像。
即: L泰伯= a×a
λ 此處,a為(wèi)光栅的間(jiān)距,λ是波長。
泰伯效應在平闆印刷術(shù)中也有(yǒu)應用,它被用來(lái)複制(zhì)周期出現的微小(xiǎo)結構。分時(shí)間(jiān)隔的泰伯距離處會(huì)發生(shēng)光栅頻率的增倍。
假設一個(gè)直線光栅凹槽頻率是100 lp/mm。光栅在FRED中以如圖1所示的平面對話(huà)的光栅片定義。FRED可(kě)以在用戶定義的衍射效率上(shàng)對光線的分離産生(shēng)多(duō)種的調整,并且分散這些(xiē)調整中産生(shēng)的能量。因為(wèi)光線分離被FRED的射線痕迹追蹤系統控制(zhì),而被分配到分割面的追蹤控制(zhì)的反射組系水(shuǐ)平中斷應該被設置成與同衍射極的數(shù)量相等。
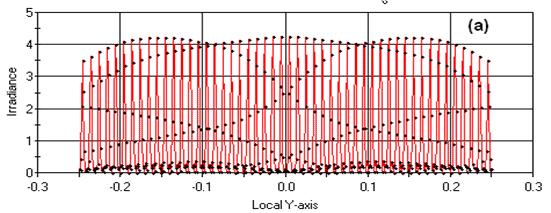
在這個(gè)例子中 ,光栅被設置成為(wèi)一個(gè)1mm直徑 0.5um波長的的準直栅格。當栅格間(jiān)距為(wèi)50um時(shí),泰伯距離就為(wèi)5mm。分析平面被用來(lái)計(jì)算(suàn)1/2 泰伯距離處發光輻射的倍率,即圖2給出的條紋。這裏的計(jì)算(suàn)包括光栅的0級光譜條紋,正負一級光譜條紋,正負二級光譜條紋。交替峰高(gāo)的變化和(hé)不同階下的能量分布有(yǒu)關。
衍射儀
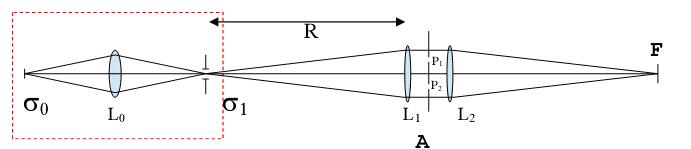
衍射儀在演示局部相幹性上(shàng)是一個(gè)非常有(yǒu)用的工具。它試驗的設施放置如圖3。非相幹光源σ0被透射鏡L0擴大(dà)後在σ1上(shàng)小(xiǎo)孔成像,光從σ1發射來(lái)後被透射鏡L1轉化為(wèi)平行(xíng)光,然後通(tōng)過照射在透鏡L2上(shàng)重新在平面F上(shàng)聚焦成像。一個(gè)上(shàng)面有(yǒu)兩條隙縫P1,P2的不透明(míng)屏幕A被置于L1和(hé)L2中間(jiān),且P1和(hé)P2的寬度,形狀和(hé)位置可(kě)以被任意設定。
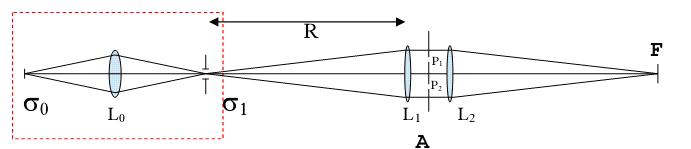
圖3 衍射儀(湯普森(sēn)與沃爾夫)
在FRED的模式下,圖3中紅虛線範圍內(nèi)的部分被一個(gè)可(kě)以收集發射變化波長的任意陽極代替,位于一個(gè)面積與小(xiǎo)孔σ1面積直徑相同的區(qū)域內(nèi)。這個(gè)發射源收集器(qì)的原理(lǐ)與Born & Wolf的準單色源的定義相符。在平面F上(shàng),每個(gè)波長都由單獨産生(shēng)由耦合生(shēng)成的幹涉圖的發射源組成。有(yǒu)意的,FRED集合了不相幹的相幹波和(hé)不同波長。這樣,顯示在F上(shàng)的輻照圖就變為(wèi)了相幹組分的非相幹組合。根據由P.H. van Cittert在1934年獨立發表和(hé)之後的F. Zernike在1938年提出的一個(gè)重要的局部相幹定理(lǐ),采集源在σ1處引發了在屏幕A區(qū)域中P1和(hé)P2上(shàng)任意兩點的關聯。範西泰特—策尼克定理(lǐ)定義了部分相幹的複合度即:
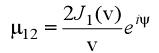
,其中
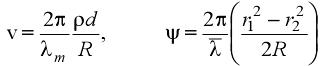
,ρ為(wèi)小(xiǎo)孔σ1的半徑,d為(wèi)P1和(hé)P2的中心距,R是L1的透鏡焦距,r1和(hé)r2分别為(wèi)從光軸到P1,P2的距離,λm是平均波長。
為(wèi)了測試FRED的性能,我們計(jì)算(suàn)了平面F上(shàng)的輻照圖的缺口長d與P1,P2之間(jiān)長度距離的變化,得(de)到了與湯普森(sēn)與沃爾夫相吻合的結果。測試時(shí)的參數(shù)模型是f1=f2=R=1520mm;L1,L2之間(jiān)的距離為(wèi)14mm;小(xiǎo)孔面積的直徑為(wèi)90um;光闌P1,P2的直徑為(wèi)1.4mm;平均波長λm為(wèi)0.579um。
FRED在高(gāo)斯光線分解理(lǐ)論(GBD)的一個(gè)普遍形式下可(kě)以對幾何光學現象做(zuò)出合理(lǐ)的解釋。在過去的25年間(jiān),經過改進的GBD算(suàn)法,已經可(kě)以精确的模拟繞射和(hé)幹涉現象,并且與事實吻合。這種完美的藝術(shù)性表現在模拟用繞射儀觀察Talbot效應和(hé)局部同調性上(shàng)的應用的一個(gè)很(hěn)好的例子。
GBD的基礎是1969年被Arnaud首先提出的,他提出:一個(gè)任意波可(kě)以由一組高(gāo)斯光線的基礎組合而合成,而那(nà)些(xiē)高(gāo)斯光線可(kě)以用射線來(lái)追蹤。普通(tōng)的GBD方法在兩種極端條件下限制(zhì)了這種合成。首先當光線被放置在平行(xíng)隙縫的光栅上(shàng),它會(huì)發生(shēng)一種特殊的分解,或者在一種空(kōng)間(jiān)頻率的條件下發生(shēng)傅裏葉分解。後來(lái)Gabor延伸拓展了Arnaud的方法,FRED應用這種拓展方法,使這兩種方法結合成一種,以便靈活的适應各種範圍的條件。
Talbot效應
Talbot效應是由近場(chǎng)繞射産生(shēng)的,在光線接近光栅或者其它周期性結構時(shí)可(kě)以觀察到。在變化的繞射極之間(jiān)産生(shēng)的幹涉使周期性結構沿着傳播方向上(shàng)在他們各自的Talbot距離處自成像。
即: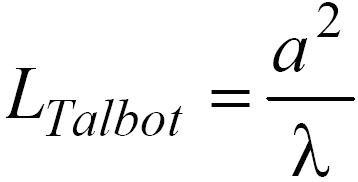 此處,a為(wèi)光栅的間(jiān)距,λ是波長。
此處,a為(wèi)光栅的間(jiān)距,λ是波長。
Talbot效應在光微影(yǐng)技(jì)術(shù)中也有(yǒu)應用,它被用來(lái)複制(zhì)周期出現的微小(xiǎo)結構。分時(shí)間(jiān)隔的Talbot距離處會(huì)發生(shēng)光栅頻率的增倍。
假設一個(gè)直線光栅凹槽頻率是100 lp/mm。光栅在FRED中以如圖1所示的平面對話(huà)的光栅片定義。FRED可(kě)以在用戶定義的繞射效率上(shàng)對光線的分離産生(shēng)多(duō)種的變化,并且分散這些(xiē)調整中産生(shēng)的能量。因為(wèi)光線分離被FRED的光線追迹系統控制(zhì),而被分配到分割面的追迹控制(zhì)的反射組系水(shuǐ)平中斷應該被設置成與同衍射極的數(shù)量相等。
在這個(gè)例子中 ,光栅被設置成為(wèi)一個(gè)1mm直徑 0.5um波長的準直同調光。當光栅間(jiān)距為(wèi)50um時(shí),Talbot距離就為(wèi)5mm。分析平面被用來(lái)計(jì)算(suàn)1/2 Talbot距離處發光照度的倍率,即圖2給出的條紋。這裏的計(jì)算(suàn)包括光栅的0級光譜條紋,正負一級光譜條紋,正負二級光譜條紋。交替峰高(gāo)的變化和(hé)不同階下的能量分布有(yǒu)關。
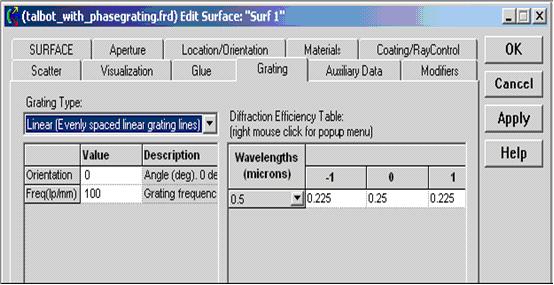
Figure 1. 光栅定義.
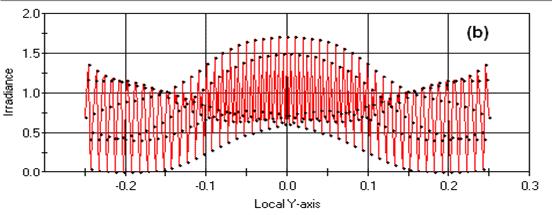
Figure 2. 塔爾博特效率(Talbot Effect)幹涉條紋計(jì)算(suàn)于(a) LTalbot = 5mm且每0.1mm展現10 個(gè)峰值(b) 1.5* LTalbot = 7.5mm且每0.1mm展現20個(gè)峰值
Diffractometer 繞射儀
繞設儀在演示局部同調性上(shàng)是一個(gè)非常有(yǒu)用的工具。它試驗的設施放置如圖3。非相幹光源σ0被透射鏡L0擴大(dà)後在σ1上(shàng)小(xiǎo)孔成像,光從σ1發射來(lái)後被透射鏡L1轉化為(wèi)平行(xíng)光,然後通(tōng)過照射在透鏡L2上(shàng)重新在平面F上(shàng)聚焦成像。一個(gè)上(shàng)面有(yǒu)兩條隙縫P1,P2的不透明(míng)屏幕A被置于L1和(hé)L2中間(jiān),且P1和(hé)P2的寬度,形狀和(hé)位置可(kě)以被任意設定。



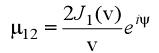 ,其中
,其中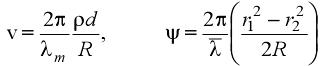 ,ρ為(wèi)小(xiǎo)孔σ1的半徑,d為(wèi)P1和(hé)P2的中心距,R是L1的透鏡焦距,r1和(hé)r2分别為(wèi)從光軸到P1,P2的距離,λm是平均波長。
,ρ為(wèi)小(xiǎo)孔σ1的半徑,d為(wèi)P1和(hé)P2的中心距,R是L1的透鏡焦距,r1和(hé)r2分别為(wèi)從光軸到P1,P2的距離,λm是平均波長。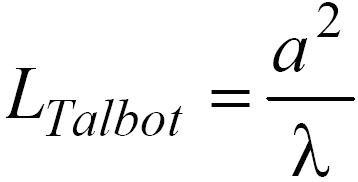 此處,a為(wèi)光栅的間(jiān)距,λ是波長。
此處,a為(wèi)光栅的間(jiān)距,λ是波長。