文章來(lái)源:Bäuerle A, Bruneton A, Wester R, et al. Algorithm for irradiance tailoring using multiple freeform optical surfaces[J]. Optics express, 2012, 20(13): 14477-14485.
主要內(nèi)容:本文基于最優化質量傳遞(optimal mass transport)多(duō)自由曲面光學的設計(jì)算(suàn)法,結合照明(míng)設計(jì)軟件FRED模拟了洗牆燈實例。使用該算(suàn)法,可(kě)直接調整多(duō)面光學系統(在本文中,我們用了雙邊自由曲面)獲得(de)了近似于預先确定照度分布,而同時(shí)可(kě)捕獲從光源發出的大(dà)部分光線。增加多(duō)曲面自由度可(kě)用來(lái)減小(xiǎo)菲涅爾損失,包含加工上(shàng)的約束以及減小(xiǎo)零件尺寸。
Axel Bauerle, 1, 2 Adrien Bruneton, 1∗ Rolf Wester, 2
Jochen Stollenwerk, 1, 2 and Peter Loosen1, 2
1Chair for the Technology of Optical Systems, RWTH Aachen University, 52056 Aachen,
Germany
2Fraunhofer Institute for Laser Technology ILT, Steinbachstr. 15, 52074 Aachen, Germany
摘要
自由曲面透鏡和(hé)反射鏡的設計(jì)能夠獲得(de)非徑向對稱的照度分布,且同時(shí)保持光學系統的緊湊性。對于點狀光源來(lái)說,比如LED,為(wèi)了增加發光效率往往需要捕獲一個(gè)寬角度的光源。這樣往往導緻的結果是産生(shēng)強彎曲光學元件,需要兩個(gè)透鏡面作(zuò)用于總的光的折射,從而最小(xiǎo)化菲涅爾損失。在本篇文章中,我們報道(dào)了一個(gè)基于最優化質量傳遞(optimal mass transport)多(duō)自由曲面光學的設計(jì)算(suàn)法,并結合光學工程仿真軟件FRED對一般照明(míng)問題給出了應用實例。
1.前言
在照明(míng)應用中,透鏡和(hé)反射鏡可(kě)以以一種預先确定的方式上(shàng)分配光線,市場(chǎng)上(shàng)對這種透鏡及反射鏡的需求越來(lái)越多(duō)。為(wèi)了獲得(de)常用的光分布,光學設計(jì)中自由度數(shù)量必須高(gāo)于傳統的光學元件,這就引入了自由曲面光學的概念,對此有(yǒu)衆多(duō)設計(jì)算(suàn)法提出[1-5]。折射式光學元件(透鏡)在材料-空(kōng)氣界面會(huì)遇到菲涅爾反射,控制(zhì)其精準的路徑來(lái)避免損失難度較大(dà)。因為(wèi)随着光線角度傾斜菲涅爾反射在增加,因此理(lǐ)想情況是使用幾個(gè)自由曲面來(lái)增加系統的光學效率,在這種情況下,一個(gè)單透鏡面足以調整照度分布。
到目前為(wèi)止文獻中發布的設計(jì)算(suàn)法,隻有(yǒu)Minano、Benıtez[5]提出的SMS3D方法可(kě)以直接裁剪多(duō)平滑表面,且同時(shí)獲得(de)預定的照度分布,甚至在一定程度上(shàng)可(kě)把擴展光源考慮進去。然而,據作(zuò)者所知,SMS3D算(suàn)法隻是在他們團隊內(nèi)部使用。對于點光源的情況,Ries 和(hé)Muschaweck[2]得(de)出了一組偏微分方程來(lái)描述單個(gè)光學面,但(dàn)一般對于多(duō)光學表面目前還(hái)沒有(yǒu)報道(dào)。
在本文中,基于傳輸理(lǐ)論的公式[6],對兩個(gè)自由曲面和(hé)一個(gè)點光源發射器(qì)的照度調整問題,我們提出了靈活的近似解算(suàn)法。此外,我們利用FRED軟件演示了對于一般照明(míng)設計(jì)任務的可(kě)行(xíng)性。
2.光線映射:有(yǒu)關光學設計(jì)的傳輸理(lǐ)論
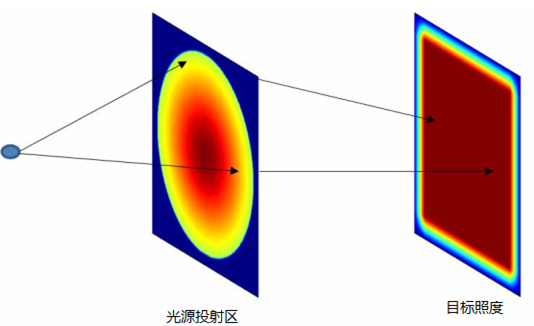
在一般的公式中,質量傳輸理(lǐ)論講述了最優路徑的計(jì)算(suàn),此計(jì)算(suàn)允許從初始質量分布到目标質量分布的連續傳遞。就光學而言,光通(tōng)量扮演了重要的角色,投射光源描述為(wèi)在2維空(kōng)間(jiān) 上(shàng)光通(tōng)量密度 (圖1)。類似的,目标空(kōng)間(jiān) 上(shàng)的光通(tōng)量密度為(wèi) 。為(wèi)了清楚起見,在3維空(kōng)間(jiān)中,假定 平行(xíng)于2維平面,光通(tōng)量密度 和(hé) 在各自的局部笛卡爾坐(zuò)标(x,y)下被參數(shù)化(圖1)。
圖1.映射計(jì)算(suàn)圖,點光源投射到平面 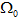 及目标照度投射到 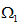 ,自由曲面位置在 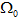 和(hé) 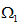 之間(jiān)。
光學系統(自由曲面)的設計(jì)任務相當于發現一個(gè)微分同胚映射(光線映射),以便于照度分布轉換匹配目标分布:
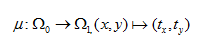 (1)
(tx,ty)代表了光源光線透過 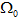 上(shàng)的(x,y)在 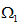 上(shàng)的目标點。因為(wèi)沿着無窮小(xiǎo)燈管從光源到探測目标上(shàng)光通(tōng)量守恒,照度轉換公式可(kě)以寫為(wèi):
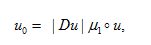 (2)
Du是u的雅克比行(xíng)列式,表示沿着路徑燈管橫截面的壓縮或放大(dà), 是常用的算(suàn)子符号。在整個(gè)平面 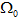 上(shàng)積分此公式得(de)到了總的能量守恒關系 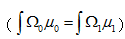 。
因為(wèi)映射u并不是獨一無二的[7],在光學設計(jì)任務中主要的限制(zhì)是發現可(kě)引導光學表面連續可(kě)微的映射。這也就是所謂的表面法向矢量N可(kě)積條件[8]
N*curl(N)=0 (3)
計(jì)算(suàn)強制(zhì)滿足方程(3)的光線映射并不是簡單的事情,因為(wèi)由雅克比判決式(Monge-Ampere-type 方程)可(kě)知方程(2)一般等效于非線性二階偏微分方程。處理(lǐ)兩個(gè)光學表面而不是一個(gè)光學表面使這個(gè)問題更具挑戰性。
3.近似最優化光線映射
表面法線矢量場(chǎng)直接關系到映射信息(通(tōng)過斯涅耳折射定律)。因此,即使現在還(hái)沒有(yǒu)被證實,看起來(lái)似乎是可(kě)信的:如果光線映射的旋度自身減小(xiǎo),表面法線矢量場(chǎng)的旋度可(kě)大(dà)幅度減小(xiǎo)。
使用最新的質量傳遞理(lǐ)論有(yǒu)助于實現這一目标。在處理(lǐ)預定的目标函數(shù)這方面大(dà)部分的工作(zuò)集中在尋找最佳映射。每個(gè)元件的位移、質量權重是具有(yǒu)代表性的二次函數(shù)。幾種不同的解決問題的方法已經被提出[9]。本文中,我們關注于在圖像變換的背景下由Haker提出的一階、無參數(shù)方案[7]。
點光源的光通(tōng)量分布投射到方形的2維空(kōng)間(jiān) 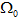 ,因此獲得(de)了平坦的光通(tōng)量密度μ。一個(gè)改進的立體(tǐ)投影(yǐng)通(tōng)常用于獲得(de)這個(gè)通(tōng)量密度,與此同時(shí)控制(zhì)可(kě)捕獲光錐角度。同樣的目标上(shàng)的光通(tōng)量分布投射到一個(gè)平行(xíng)的方形區(qū)域 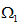 。如圖1所示。
Haker的步驟[7]是首先找到μ0和(hé)μ1初始映射關系(通(tōng)常是在笛卡爾坐(zuò)标軸上(shàng)兩個(gè)連續1維數(shù)值積分),初始映射結果用 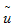 表示。
Haker演示了μ0和(hé)μ1所有(yǒu)映射可(kě)用連續變量t表示,同樣的,u可(kě)以看作(zuò)t的函數(shù), 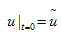 。通(tōng)量符合如下演化方程:
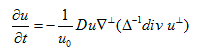 (4)
Du表示映射的雅克比行(xíng)列式, 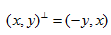 代表在二維空(kōng)間(jiān)旋轉90度, 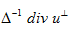 是f的解,表示為(wèi)泊松公式 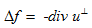 。
這個(gè)方程的穩态解(當t--->∞ )已經被Haker證明(míng)了是二次型性能指标最優化映射。本文中,此方程的解使用Hakert數(shù)值技(jì)術(shù),使用 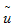 作(zuò)為(wèi)初始點。注意演化方程本身不使用μ1作(zuò)為(wèi)相關信息,因為(wèi)它已經包含在初始映射 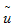 裏面了。
用這種方法減小(xiǎo)映射的旋度會(huì)得(de)到一個(gè)好的積分近似條件,如下面第五部分所示。
4.由光線映射構建光學表面
使用映射信息,光學表面的計(jì)算(suàn)可(kě)促使光源光線偏轉到想要的目标位置。總的光的偏轉分成幾個(gè)部分(在如下的例子中描述了兩種),對于一個(gè)給定的光學面,每個(gè)都可(kě)實現。在本文中,構建方法是使用标準的最小(xiǎo)二乘優化法。表面使用三角形網格畫(huà)法頂點為(wèi)i=1,……N,他們的位置為(wèi)由下列式子給出:
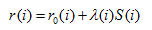 (5)
r0(i)是光線i的起點,可(kě)以是點光源的位置或光線通(tōng)過另一個(gè)光學面的位置。S(i)是光線的方向矢量,λ(i)是标量參數(shù)定義表面點i。
S(i)和(hé)N(i)給出了光線折射或反射後方向矢量S0(i)。法向矢量N(i)在三角形面頂點位置由頂點相鄰面法向平均加權計(jì)算(suàn)得(de)到。
鑒于S0(i)、光線在光學面上(shàng)的位置r(i)、光線交于目标面的點T(i)都可(kě)以計(jì)算(suàn)。由下式(6)最小(xiǎo)化作(zuò)為(wèi)目标函數(shù)
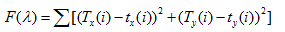 (6)
Tx(i)和(hé)Ty(i)是給定的參數(shù)矢量 的光線局部目标面的坐(zuò)标,tx(i)和(hé)ty(i)分别是映射算(suàn)法中想得(de)到的局部目标坐(zuò)标。
表面構建是基于目标面上(shàng)的光線坐(zuò)标符合積分條件。算(suàn)法與在目标面上(shàng)的光線位置協調進行(xíng),因此可(kě)在多(duō)個(gè)光學表面偏轉光線,引入額外的自由度到設計(jì)上(shàng)而并非算(suàn)法上(shàng),因為(wèi)算(suàn)法隻考慮單個(gè)面。
使用三角網格算(suàn)法的優勢體(tǐ)現在可(kě)非常靈活的進一步處理(lǐ)結果表面。例如他們可(kě)以細化處理(lǐ)或快速切割,因此,引入了出色的透鏡邊界控制(zhì)條件。結合多(duō)面設計(jì)允許包含加工限制(zhì)條件(如注塑成型可(kě)避免凹陷)。
5.建築照明(míng):洗牆燈實例應用
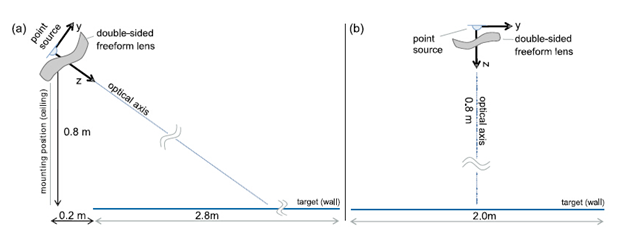
圖2給出了标準的、高(gāo)光學效率,建築照明(míng)上(shàng)具有(yǒu)挑戰性幾何結構,吸頂燈距離均勻照度接受面80cm。第一步,建立一個(gè)簡單的軸上(shàng)演示設計(jì),并對比了傳統的非-優化的映射(1維逐次積分)設計(jì)。基于此,建立了更具有(yǒu)挑戰性的傾斜設計(jì)。
圖2.(a)自定義坐(zuò)标軸的洗牆燈應用 (b)簡單的軸上(shàng)方案
5.1 軸上(shàng)實例
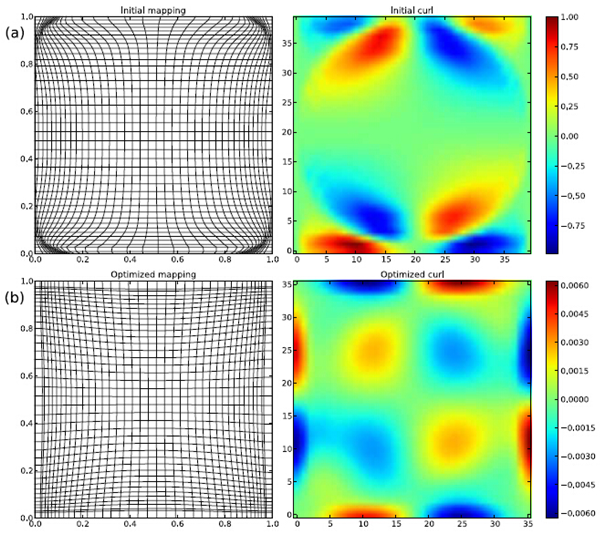
依據上(shàng)面列出的算(suàn)法,一個(gè)初始的光線映射計(jì)算(suàn)出來(lái),并構建了相應的光學表面結構(假設材料是PMMA,n=1.49),最小(xiǎo)化目标函數(shù)(公式6)。為(wèi)完善設計(jì),對如上(shàng)的初始映射進行(xíng)了優化,第二組表面随後被構建。圖3給出了相應的映射,分别表示為(wèi)規則網格的變形及z分量的旋度。當系數(shù)為(wèi)200時(shí)總的旋度量急劇(jù)減小(xiǎo)。
圖3. 光線映射(表示為(wèi)規則網格的變形)及相應的Z分量旋度映射,(a) 優化前 (b) 優化後
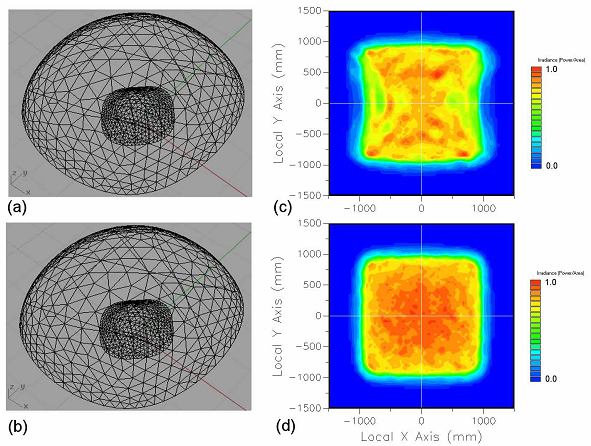
在兩種表面處執行(xíng)了蒙特卡洛光線追迹,圖4給出了每種情況的最終照度分布。500萬條光線、目标面上(shàng)探測器(qì)分辨率點為(wèi)71*71,所有(yǒu)的這些(xiē)均由FRED[10]光學工程仿真軟件來(lái)完成。光源是标準的朗伯體(tǐ)點發射器(qì),半角分布為(wèi)70度圓錐角,方向沿着z軸。
盡管透鏡的形狀極其相似,圖4(d)中的光分布顯示了與均勻照度分布相比顯示了極小(xiǎo)的變形。證實了旋度減少(shǎo)得(de)到了令人(rén)滿意的光線映射,例如與初始映射相比更好的與積分條件(公式3)的匹配,同時(shí)更接近想要的光通(tōng)量變化。
圖.4 FRED軟件線框圖示及用蒙特卡羅光線追迹後輻照度分布(任意單位)。(a)和(hé)(c)沒有(yǒu)映射優化;(b)和(hé)(d)映射優化後 |


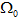 及目标照度投射到
及目标照度投射到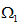 ,自由曲面位置在
,自由曲面位置在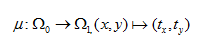 (1)
(1)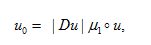 (2)
(2)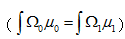 。
。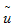 表示。
表示。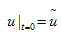 。通(tōng)量符合如下演化方程:
。通(tōng)量符合如下演化方程: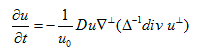 (4)
(4)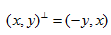 代表在二維空(kōng)間(jiān)旋轉90度,
代表在二維空(kōng)間(jiān)旋轉90度,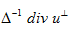 是f的解,表示為(wèi)泊松公式
是f的解,表示為(wèi)泊松公式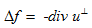 。
。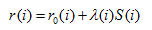 (5)
(5)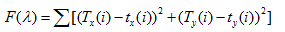 (6)
(6)