此示例演示了由不同電(diàn)介質界定的銀薄膜的等離子體(tǐ)激元波導的計(jì)算(suàn)。 該設置遵循 Berini [1] 的舉例。 我們主要評論整個(gè)計(jì)算(suàn)域上(shàng)電(diàn)場(chǎng)強度的數(shù)值解,它代表了一個(gè)等離子體(tǐ)激元。 但(dàn)是,對于傳播模式項目,也會(huì)計(jì)算(suàn)傳播常數(shù)(傳播模式)。
幾何示意圖如下:
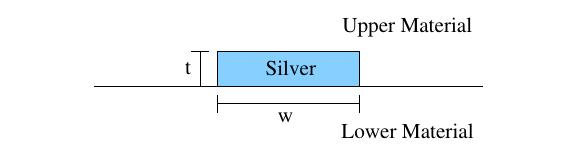
下層和(hé)上(shàng)層材料的相對介電(diàn)常數(shù)由 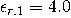 和(hé) 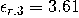 給出。這個(gè)金屬薄膜的厚度是和(hé)寬度是 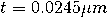 。分析了真空(kōng)波長為(wèi) 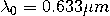 時(shí)的結構。金屬薄膜(銀)在該波長的相對介電(diàn)常數(shù)為(wèi) 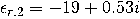 。
在本例中,我們計(jì)算(suàn)具有(yǒu)相對于波導對稱平面的鏡像對稱電(diàn)場(chǎng)的 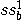 模式 [1]。 因此,隻需離散化幾何結構的一半就足夠了。經過最後一步細化後的三角形幾何部分如下圖所示。
由于金屬角附近的奇異場(chǎng)行(xíng)為(wèi)和(hé)幾何結構的多(duō)尺度結構,等離子體(tǐ)激元模式的精确計(jì)算(suàn)是一個(gè)具有(yǒu)挑戰性的問題。 等離子體(tǐ)激元的傳播主要集中在極薄銀帶附近。 自适應有(yǒu)限元離散化是解決這類問題的一種方法。 由于角的預細化和(hé)自适應細化步驟,網格被細化,特别是在靠近細帶和(hé)靠近金屬角的地方,這些(xiē)地方的電(diàn)場(chǎng)表現出奇異的行(xíng)為(wèi),必須非常精确地解決。得(de)到的結果如下圖所示:
參考文獻
[1] (1, 2)P. Berini, Plasmon-polariton waves guided by thin lossy metal films of finite width: Bound modes of symmetric structures, Phys. Rev. B 61, 10484 (1999)
|



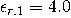 和(hé)
和(hé)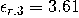 給出。這個(gè)金屬薄膜的厚度是和(hé)寬度是
給出。這個(gè)金屬薄膜的厚度是和(hé)寬度是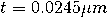 。分析了真空(kōng)波長為(wèi)
。分析了真空(kōng)波長為(wèi)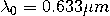 時(shí)的結構。金屬薄膜(銀)在該波長的相對介電(diàn)常數(shù)為(wèi)
時(shí)的結構。金屬薄膜(銀)在該波長的相對介電(diàn)常數(shù)為(wèi)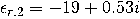 。
。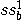 模式 [1]。 因此,隻需離散化幾何結構的一半就足夠了。經過最後一步細化後的三角形幾何部分如下圖所示。
模式 [1]。 因此,隻需離散化幾何結構的一半就足夠了。經過最後一步細化後的三角形幾何部分如下圖所示。
