利用光學手性和(hé)內(nèi)置手性參量的形式,可(kě)以在JCMsuite中計(jì)算(suàn)光學散射體(tǐ)的手性響應。結果表明(míng),時(shí)間(jiān)諧波光學手性密度服從局部連續性方程[1]。這使得(de)手性行(xíng)為(wèi)的分析類似于電(diàn)磁能量的研究。
圓偏振平面波是光手性的本征态。因此,近場(chǎng)光手性密度與圓偏振密切相關。在幾何光學中,四分之一波闆将線偏振轉換為(wèi)圓偏振是衆所周知的。它們是由雙折射材料制(zhì)成的,例如各向異性材料。波片的厚度是尋常(x-)偏振和(hé)非尋常(z-)偏振波長差的四分之一。入射平面波在xz方向上(shàng)線性偏振,在-y方向上(shàng)傳播,如下圖所示:
四分之一波片的能量守恒和(hé)光學手性
由于線偏振,入射手性通(tōng)量消失 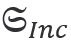 =0。對于一個(gè)完美的四分之一波片,反射通(tōng)量  将消失,而透射手性通(tōng)量 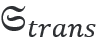 =1将以圓偏振平面波為(wèi)單位。從幾何光學的角度,我們認為(wèi)由于波片的各向異性導緻了偏振變化或手性轉換發生(shēng)在波片的體(tǐ)積 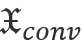 內(nèi)。對于麥克斯韋方程組的嚴格解,會(huì)産生(shēng)與這個(gè)簡化模型的輕微偏差。
在近場(chǎng)中,由于各向異性和(hé)材料參數(shù)[1]的變化而發生(shēng)手性轉換。利用各向異性電(diàn)學手性 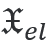 的密度積分,可(kě)以在JCMsuite中計(jì)算(suàn)體(tǐ)積貢獻。這種轉換類似于能量吸收 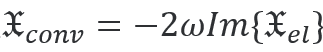 。對于這個(gè)例子中的分段常數(shù)材料,界面處的手性轉換是通(tōng)過電(diàn)磁手性轉換通(tōng)量積分來(lái)計(jì)算(suàn)的。它的實部得(de)到 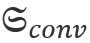 。
最後,通(tōng)過對界面外域電(diàn)磁手性通(tōng)量積分取實數(shù)部分給出了反射  和(hé)透射 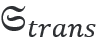 光手性通(tōng)量。由于光學手性守恒,推導出下式:
适用于任意材料和(hé)電(diàn)磁場(chǎng)。這類似于能量守恒,可(kě)寫為(wèi)
光學手性密度 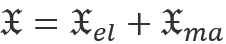 如下所示
研究了四分之一波片近場(chǎng)的光手性密度 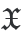  (左)及其體(tǐ)積轉換 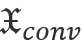 (右)
這是由輸出參量:磁性手性密度和(hé)各向異性電(diàn)性手性密度得(de)到的。在這裏,目前的符号并沒有(yǒu)區(qū)分整數(shù)(例如  或 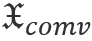 )和(hé)密度(例如 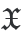 )。
注意,各向異性手性密度在計(jì)算(suàn)上(shàng)比它們的各向同性對應部分更消耗計(jì)算(suàn)資源。由于所涉及的材料是非磁性的(μr=1),計(jì)算(suàn)(各向同性)磁性手性密度就足夠了。還(hái)需要注意的是,各向異性參量僅适用于具有(yǒu)電(diàn)場(chǎng)分量或磁場(chǎng)分量的解決方案。這是由于需要對該場(chǎng)進行(xíng)額外的導數(shù)求解。
對四分之一波片近場(chǎng)(見上(shàng)圖)的分析證實了幾何光學的預期: 在周圍的空(kōng)氣中波片內(nèi)偏振變化發生(shēng) 為(wèi)零(和(hé)界面)。向下傳播(輸出)平面波的光手性密度幾乎是圓平面波手性密度的一個(gè)單位。發現輸出偏振幾乎完全圓偏振直至 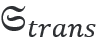 / 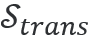 ≈0.9938。通(tōng)過優化其厚度,可(kě)以獲得(de)更優異的較低(dī)反射性能。
參考文獻
[1] (1, 2) Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756, pages 97560X. International Society for Optics and Photonics, 2016.
|


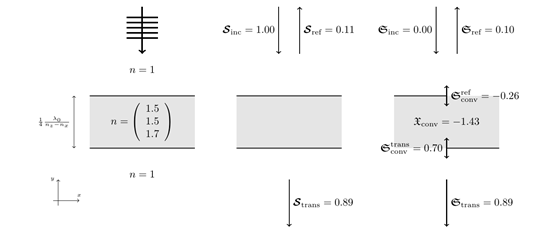
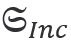 =0。對于一個(gè)完美的四分之一波片,反射通(tōng)量
=0。對于一個(gè)完美的四分之一波片,反射通(tōng)量 将消失,而透射手性通(tōng)量
将消失,而透射手性通(tōng)量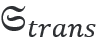 =1将以圓偏振平面波為(wèi)單位。從幾何光學的角度,我們認為(wèi)由于波片的各向異性導緻了偏振變化或手性轉換發生(shēng)在波片的體(tǐ)積
=1将以圓偏振平面波為(wèi)單位。從幾何光學的角度,我們認為(wèi)由于波片的各向異性導緻了偏振變化或手性轉換發生(shēng)在波片的體(tǐ)積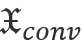 內(nèi)。對于麥克斯韋方程組的嚴格解,會(huì)産生(shēng)與這個(gè)簡化模型的輕微偏差。
內(nèi)。對于麥克斯韋方程組的嚴格解,會(huì)産生(shēng)與這個(gè)簡化模型的輕微偏差。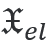 的密度積分,可(kě)以在JCMsuite中計(jì)算(suàn)體(tǐ)積貢獻。這種轉換類似于能量吸收
的密度積分,可(kě)以在JCMsuite中計(jì)算(suàn)體(tǐ)積貢獻。這種轉換類似于能量吸收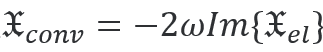 。對于這個(gè)例子中的分段常數(shù)材料,界面處的手性轉換是通(tōng)過電(diàn)磁手性轉換通(tōng)量積分來(lái)計(jì)算(suàn)的。它的實部得(de)到
。對于這個(gè)例子中的分段常數(shù)材料,界面處的手性轉換是通(tōng)過電(diàn)磁手性轉換通(tōng)量積分來(lái)計(jì)算(suàn)的。它的實部得(de)到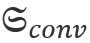 。
。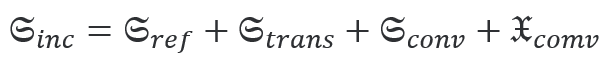
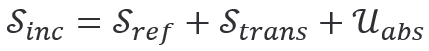
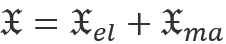 如下所示
如下所示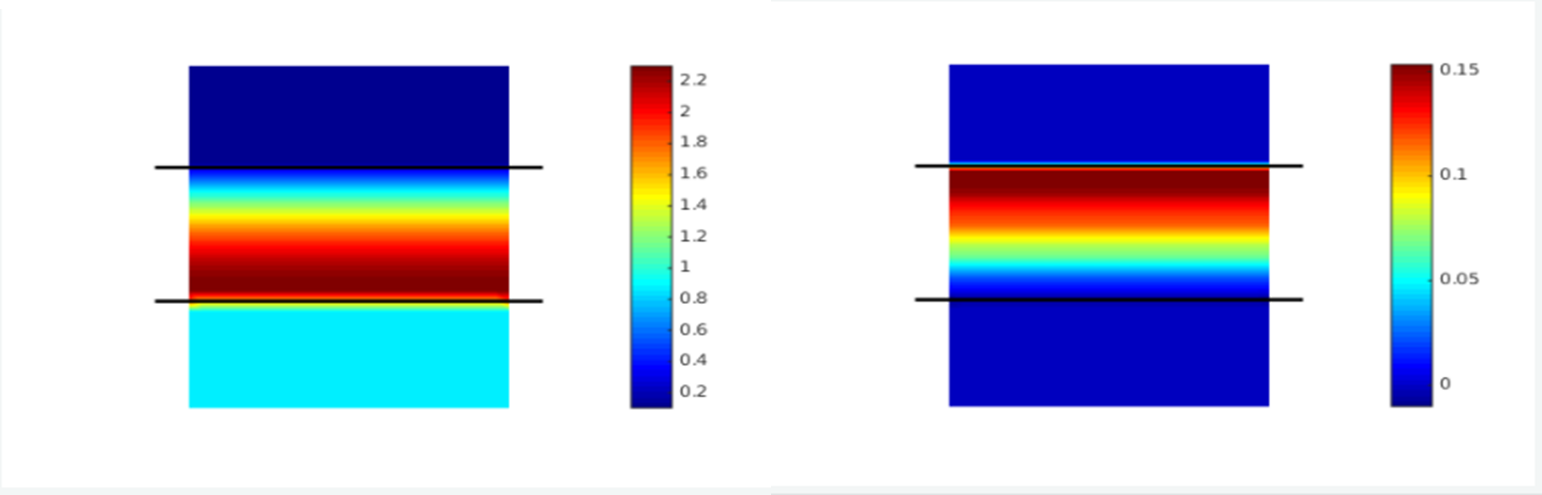
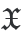
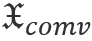 )和(hé)密度(例如
)和(hé)密度(例如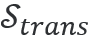 ≈0.9938。通(tōng)過優化其厚度,可(kě)以獲得(de)更優異的較低(dī)反射性能。
≈0.9938。通(tōng)過優化其厚度,可(kě)以獲得(de)更優異的較低(dī)反射性能。